Spatially resolved EELS (SR-EELS)
with an in-column Omega filter - characterization of energy filter aberrations
and their correction by image processing
Michael Entrup
version: 05.09.2014
Tested with Chromium 36.0.1985.125 on Ubuntu 14.04. This presentation may not run smooth on other systems.
impress.js - A short introduction
This presentation was created by using impress.js.
What is impress.js
It's a presentation framework based on the power of CSS3 transforms and transitions in modern browsers and inspired by the idea behind prezi.com.
[https://github.com/bartaz/impress.js]
About impress.js:
- You only need a browser and a text editor
- Uses HTML, CSS and JavaScript
- Not limited to slides
- Place your contend in a 3D canvas
A 3D canvas
- Set x-, y- and z-coordinates
- Rotate around all 3 axes
- Zoom in and out
- CSS 3D transforms from meet.js summit by @bartaz
- Testing impress.js by @manursio
- Hashdog: Software Factory - Brochure by Franco Alvarez
- Building a Personal Website with impress.js by Rakhitha Nimesh
- jgog.in Website/Portfolio of Jenil Gogari, designer from Mumbai, India
All links will open in a new tab. So have a look at all the impressive examples.
It is even possible to use LaTeX code to create formulas.
Here is an example:
When \(a \ne 0\), there are two solutions to \(ax^2 + bx + c = 0\) and they are
$$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$$
This formulas are created by MathJax.
<script type='text/javascript'>
// Say hello world until the user starts questioning
// the meaningfulness of their existence.
function helloWorld(world) {
for (var i = 42; --i >= 0;) {
alert('Hello ' + String(world));
}
}
</script>
<style>
p { color: pink }
b { color: blue }
u { color: 'umber' }
</style>
google-code-prettify is used to create this output.
To bad there is no video about the Zeiss Libra 200FE with an in-column Omega filter on youtube.
SR-EELS - An introduction
L. Reimer, I. Fromm and R. Rennekamp
We call those coordinates "dispersive" for which the one- or two-dimensional intensity distribution is recorded and use different symbols for the "selective" windows.
[Reimer1989]
| Dispersive coordinates | Selective windows |
| x, y (space coordinates) | ΔA (specimen area) |
| d (diameter of selected area) | |
| Δy (width of slit parallel to x) | |
| ΔE (energy loss) | ΔW (energy window) |
| Mode | I (dispersive/selective) |
| ESI (electron spectroscopic imaging) | I(x, y/ΔW) |
| EELS (electron energy-loss spectroscopy) | |
| Spectrum mode | I(ΔE/ΔA) |
| Space-dispersive mode | I(x, ΔE/Δy) |
- high number of lateral channels
- limited number of energy channels
- limited energy resolution
- high number of energy channels
- high energy resolution
- limited number of lateral channels
- lateral resolution can be very high
- high number of energy channels
- high energy resolution
- only one lateral axis
- high lateral resolution (x-axis)
 |
 |
- By default, only up to 25% of our camera area is used. The shown spectrum magnification (SpecMag) results in only ~8%.
- How can we increase the lateral extend?
How can we increase the lateral extend?
- projective I controls the lateral resolution (nm/px)
no effect on the size at the camera - by default, the energy-filter is not adjusted
- projective II controls the lateral and energy resolution (more details on the next slides)
SpecMag - Some quantitative values
| SpecMag value | energy range | lateral extend |
| 315 315 is the highest available value | ~83 eV | ~25% |
| 250 | ~105 eV | ~19% |
| 200 | ~130 eV | ~16% |
| 163 | ~162 eV | ~13% |
| 125 | ~212 eV | ~10% |
| 100 | ~273 eV | ~8% |
| There are some more ... | ||
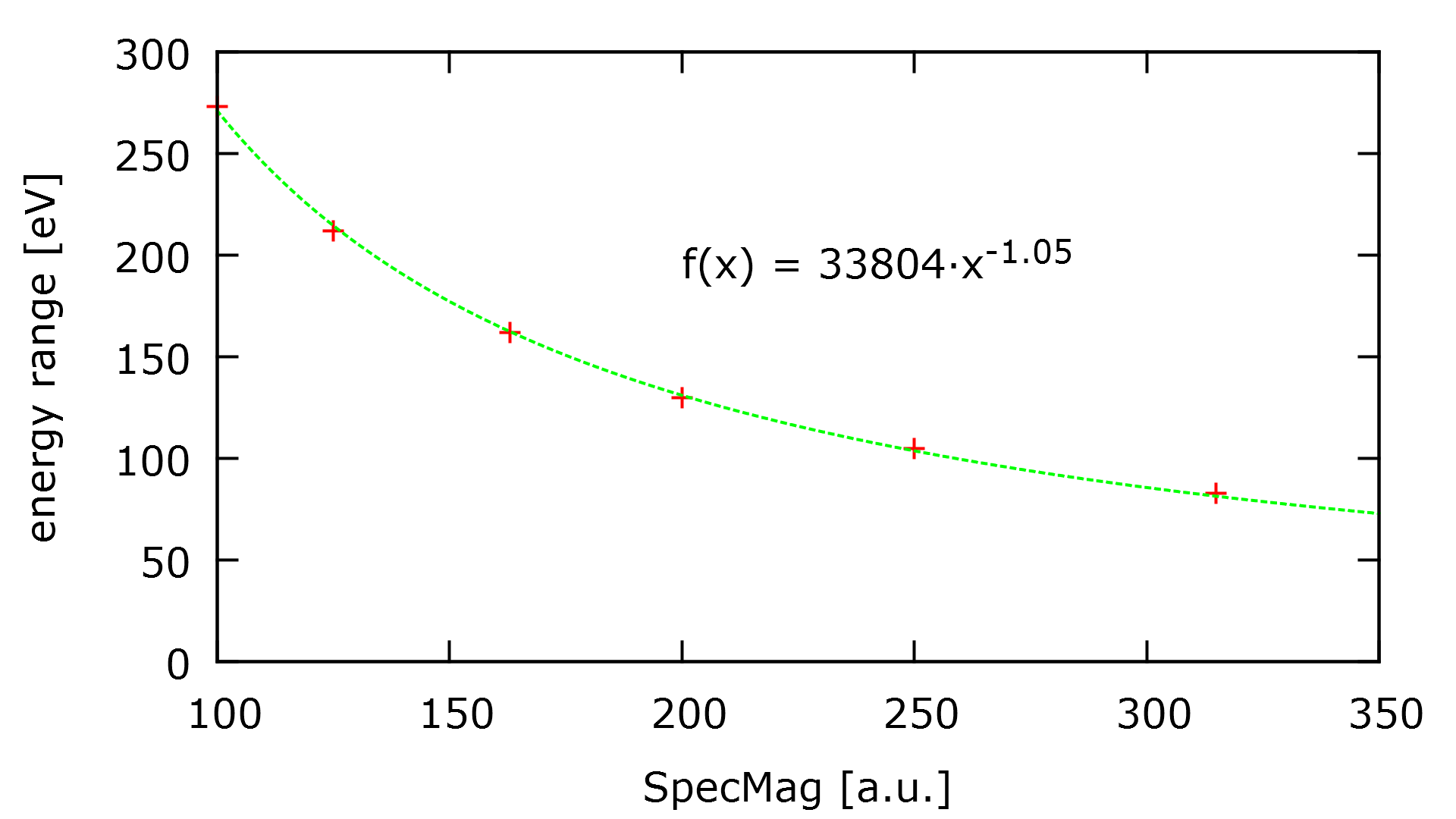
- The energy range of a single SR-EELS image
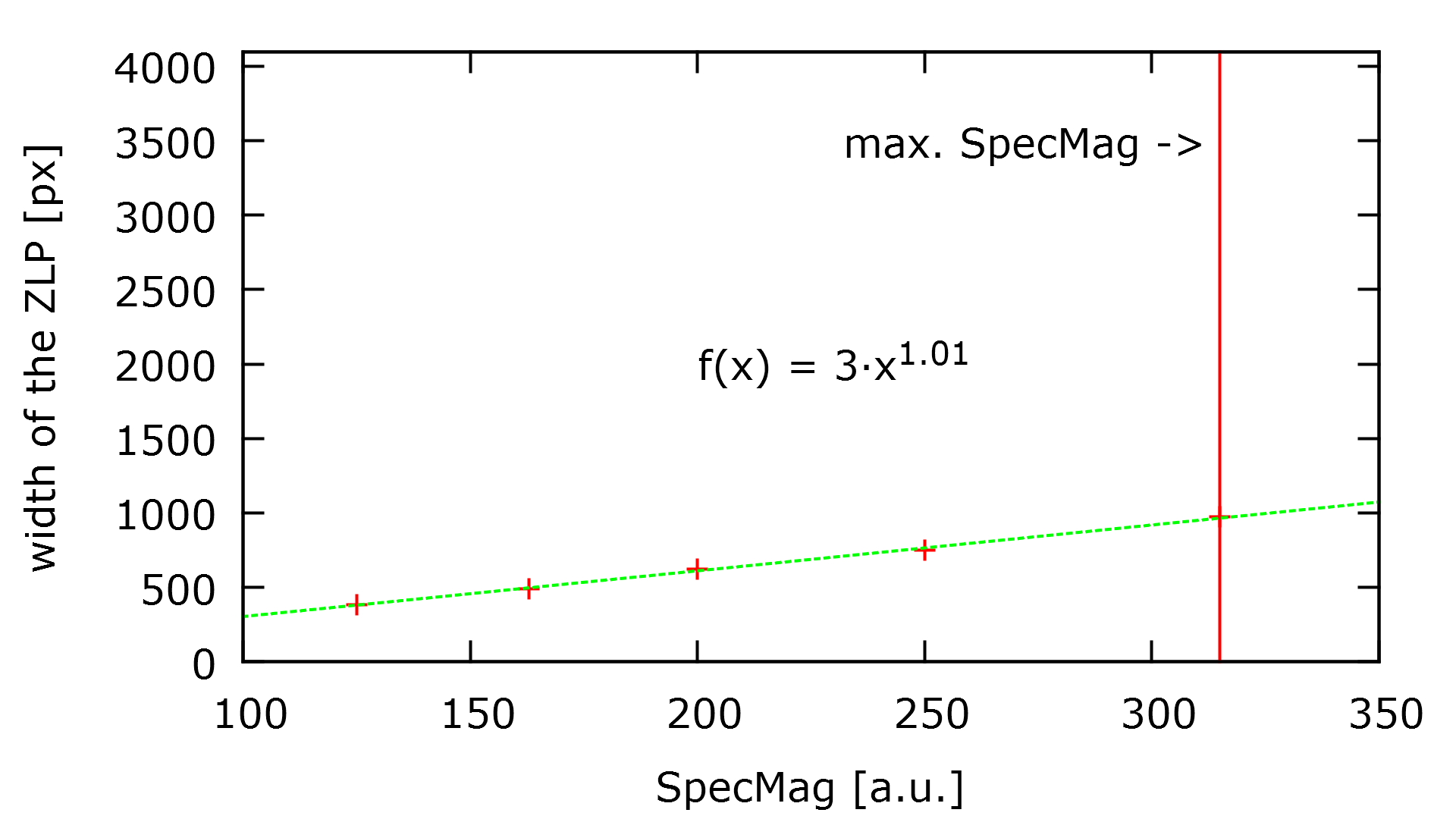
- Without touching the energy filter, there is only a limited number of lateral channels (up to ~1000 for binning 1).
Zeiss WinTEM - Energy Filter Align (EFA)
- can be found at
Service > Energy Filter... - control of 7 filter elements
- 4 dipole elements
-> shift the spectrum - 3 quadrupole elements
-> deform and rotate the spectrum - deform means to compress or expand the spectrum in lateral direction
- deform x (QSinK7): increase the lateral size
- deform y (QSinK4): controls the focus of this axis
- rotation (QCosK4)
 |
 |
- The optimized value of QSinK7 increases the lateral magnification by about 10 times.
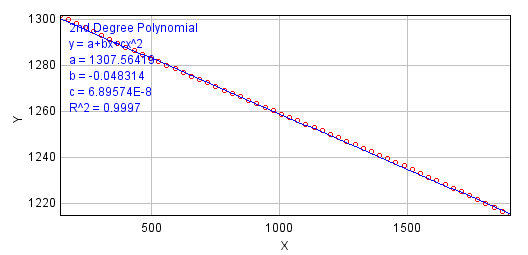
Aberrations
- The lateral extend decreases with increasing energy loss
- This aberration is visible at all previous images
- Described by a polynomial of 2nd (3rd) degree
 |
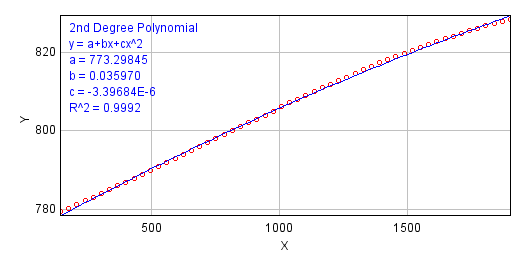 |
| (This plots were automatically created by SR-EELS_characterisation.ijm and they are only used to check the tabulated results.) | |
- How can we characterise the aberrations?
- Select a small aperture at the filter entrance plane.
- Shift the aperture perpendicular to the energy dispersive direction.
- Record a SR-EELS image at several positions of the aperture.


The red line bisects the camera area.
The marks at the borders and the centre of the signal were automatically created by SR-EELS_characterisation.ijm.
- Detection of the spectrum borders and the centres.
- For intervals of 64 energy channels (adjustable).
- The ImageJ macro uses a combination of a Gaussian fit and the build-in threshold routine.
ΔE-pos;x-pos;top;bottom;width;bottom-top 287.268;2073.198;2027;2119;92.406;92 351.320;2072.148;2026;2117;91.859;91 415.333;2071.055;2025;2116;91.234;91 479.405;2069.943;2024;2114;90.046;90 543.446;2068.870;2024;2113;89.218;89 607.375;2067.873;2023;2111;88.093;88 671.393;2066.938;2023;2110;87.687;87 735.432;2066.045;2022;2108;86.015;86 799.484;2065.081;2022;2107;85.234;85 863.452;2064.225;2021;2106;84.546;85 927.518;2063.320;2021;2105;84.234;84 991.614;2062.567;2021;2103;82.453;82 1055.533;2061.728;2020;2102;81.500;82 ...
- The results are saved in files that look like this.
_SpecMag=315_QSinK7=0_225eV.png)
- There is not only a decrease in width with increasing energy loss.
- The width decreases on the lateral axis, too.
_SpecMag=315_QSinK7=0_225eV.png)
$$w(\Delta E,x) = \sum^2_{i,j=0}a_{ij}\cdot \Delta E^i x^j$$ fits nearly perfect.
- The lateral extend decreases with increasing energy loss
- This aberration attracts attention at all SR-EELS images
- Described by a polynomial of 2nd degree
- The lateral width changes at each energy channel
- Highest value at the centre
- The decrease limits the field of view
- Described by a polynomial of 2nd degree
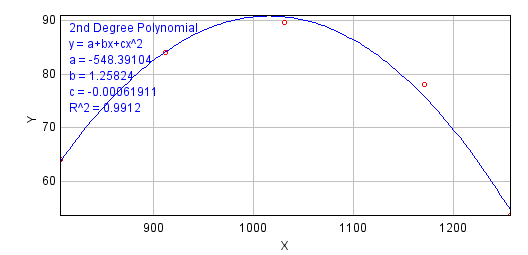
- We can try to present the results using only a 2D graph. This represents the aberration on the camera.
- A single function is used to fit all spectrum borders:
$$\tilde{x}(\Delta E) = \sum^2_{i,j=0}a_{ij}\cdot\Delta E^i\cdot x_0^j,$$
where \(x_0\) is the x-value of a spectrum border at \(\Delta E=0\). - Mathematically this is a function series:
$$f:\mathit{D}\ \mathsf{x}\ \mathbb{N} \to \mathit{Z}, \quad (x,n) \mapsto f_n(x).$$ - This does not fully describe the aberration. The missing step is presented at the next section.
- Two functions are necessary to fully describe the aberration. $$w(\Delta E,x) = \sum^2_{i,j=0}a_{ij}\cdot \Delta E^i x^j \textsf{ and}$$ $$\tilde{x}(\Delta E) = \sum^2_{i,j=0}a_{ij}\cdot\Delta E^i\cdot x_0^j,$$
- We need to combine both results to correct the SR-EELS images.
Correction by image processing
- To correct a SR-EELS image we need to transform the image coordinates.
- The resulting image must have rectangular axes \(\Delta E\) and \(x\).
- The curved axes \(\Delta \tilde{E}\) and \(\tilde{x}\) are recorded with a non curved detector.
- We assume that the top image is the corrected SR-EELS image.
- With \(\tilde{x}(\Delta E)\) and \(w(\Delta E, x)\) we can transform this image to fully visualise the aberration.
- If the energy loss is affected by the curved axes, we can transform it by calculating the arc length.
$$\Delta \tilde{E} = s_{\tilde{x}}(\Delta E) = \int_0^{\Delta E} \sqrt{1+\left(f_{\tilde{x}}'(z)\right)^2}\mathrm dz$$
$$\mathrm{with\quad} a = 4a_2^2\mathrm{,\quad } b = 4a_1a_2 \mathrm{\quad and\quad } c = a_2^2+1$$
$$\mathrm{and\quad} a_h = a_{h0} + a_{h1}\cdot x_0 + a_{h2}\cdot x_0^2$$
$$\Rightarrow \Delta \tilde{E}(\Delta E) = \int_0^{\Delta E} \sqrt{a\cdot z^2+b\cdot z+c}\,\mathrm dz$$
- \(\Delta \tilde{E}\) is the "real" energy offset.
- The inverse function is the projection of \(\Delta \tilde{E}\) on the \(\Delta E\)-axis.
$$\Delta \tilde{E}(\Delta E) = \int_0^{\Delta E} \sqrt{a\cdot z^2+b\cdot z+c}\,\mathrm dz$$
$$\mathrm{with\quad} g'(y) = \frac{1}{f'(x)}\quad and\quad g(y) = f^{-1}(y)$$
$$\Rightarrow \Delta E = s^{-1}(\Delta \tilde{E}) = \int_0^{\Delta \tilde{E}} \frac{\mathrm dz}{\sqrt{az^2+bz+c}}$$
- An analytical solution of this integral can be found at an integral table.
- There are three solution for different intervals of the parameters \(a\), \(b\) and \(c\). Only one solution is valid for this case.
$$\Delta E(\Delta \tilde{E}) = \int_0^{\Delta \tilde{E}} \frac{\mathrm dz}{\sqrt{az^2+bz+c}}$$
$$\Rightarrow\Delta E(\Delta \tilde{E}) = \left.\frac{1}{\sqrt{a}}\mathrm{arcsinh}\frac{2az+b}{\sqrt{4ac-b^2}}\right|^{z=\Delta \tilde{E}}_{z=0}$$
$$\mathrm{for\quad }4ac-b^2 = 4a_2^2\cdot(7a_1^2 + 11) > 0$$
\(\Delta E\)-coordinate:
$$\Delta E(\Delta \tilde{E}) = \left.\frac{1}{\sqrt{a}}\mathrm{arcsinh}\frac{2az+b}{\sqrt{4ac-b^2}}\right|^{z=\Delta \tilde{E}}_{z=0}$$
$$= \frac{1}{\sqrt{a}}\left(\textrm{arcsinh}\frac{2\,a\cdot\Delta \tilde{E}+b}{\sqrt{4\,ac-b^2}} - \textrm{arcsinh}\frac{b}{\sqrt{4\,ac-b^2}}\right)$$
$$\mathrm{with\quad } a = 4\,a_2^2\mathrm{,\quad } b = 4\,a_1a_2 \mathrm{\quad and\quad } c = a_2^2+1$$
\(x\)-coordinate:
$$x = f_{\tilde{x}}(\Delta \tilde{E}) = a_2\cdot \Delta \tilde{E}^2+a_1\cdot \Delta \tilde{E}+a_0$$
The revision of this presentation is not yet finished. The following section is only a draft version.




-
The size of each pixel changes.
\(\Rightarrow\)The intensity per pixel changes accordingly. - A corrected pixel will overlay several uncorrected pixels.
Details are presented at the blackboard!
- The imaging filter can be adjusted by several controls, but only QSinK7 (deform x) and QSinK4 (deform y) are useful.
- The lateral magnification can be adjusted independently from the energy magnification.
- The distortion of the imaging filter can be described by a function series of simple polynomials of 2nd degree.
- The main problem of the correction is the mapping of calculated continuous coordinates to discrete coordinates of the recorded images.
- This presentation will be extended to give a general overview to SR-EELS at the Libra 200FE.
- The algorithm for the correction of the intensity is not yet completed. The goal is to finish it next week.
- I have to investigate if a measurement is reproducible, or if it is necessary to run the calibration procedure each time.
- An approach is required to calibrate the lateral axis
(The calibration for the energy axis can be taken from EELS mode).
Thank you for your attention!